Areas of mathematics
Mathematics, love it or hate it, it runs our world. It is the foundation of every science from computers science to biology via economy. It is the language of the universe and everything it contains. However, unless you study mathematics at a university level, you may think that math is just about numbers. That’s why I wish to present you the three main branches of mathematics : Algebra, Analysis, and Geometry/Topology. Don’t worry, the goal is not to dive into the complexity of the domains but rather to give you a sense of their scope.
Algebra (Study of mathematical structures)
Algebra is the study of mathematical structures and the rules for how they interact; it is the study of formulae, equations, … It is the study of how to write math.
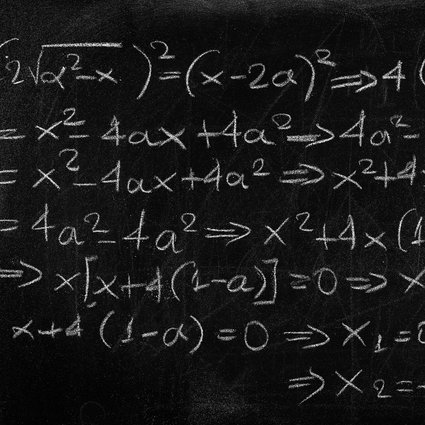
The most well-known sub-field of algebra is arithmetic; “the art of numbers”. It is the study of numbers and how they interact through operations such as addition, division, etc. It is the most popular part of math in the sense that it can be useful for everyone in their day to day lives. For example, whenever we go shopping or plan a route to some destination, arithmetic comes in handy to help us keep track of money and time spent on those activity.
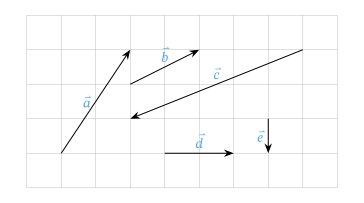
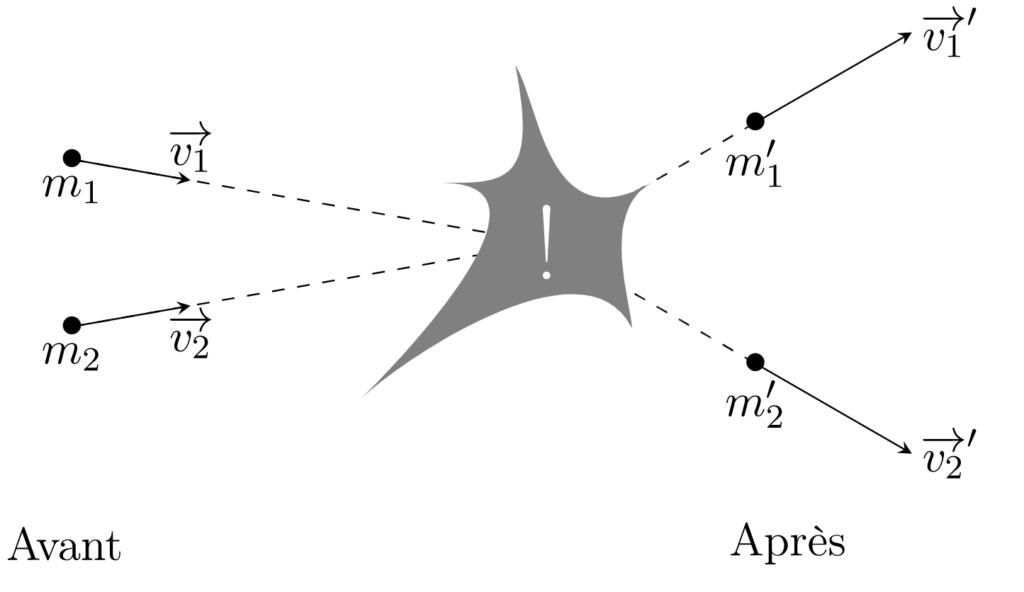
Another sub-field of algebra is linear algebra. Put simply, it is the study of vectors and how they interact. A vector describes a direction and a magnitude; they are represented as arrows. They are an essential element in modern mathematics and are used in many applications. They can be used to describe a force applied on an object, the speed of a car, or the evolution of the price of a good. In physics, for example, vectors can greatly simplify collision calculations.
Analysis (Study of changes)
Analysis is the study of change and related concepts. Analysis asks question such as : “what happens when the smallest change possible is applied?”. The smallest possible change is not zero but it is as close to zero as possible, we call this an infinitesimal change.
You might ask : What kind of changes? Changes to what? Well anything, that’s the point of math, to model everything. For example, changes in prices of goods for economist or changes of the forces applied on an objects for physicists.
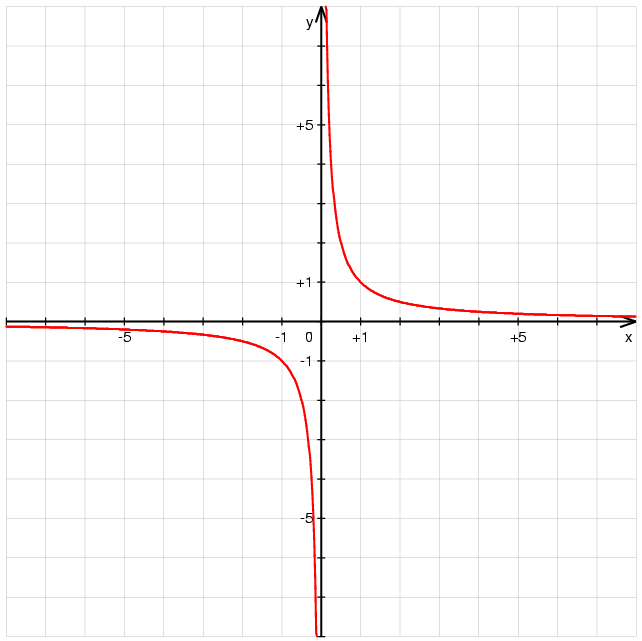
To study these changes we use limits; a value that is approachable but often unreachable. A good example is 1/x, as x gets smaller and smaller, 1/x gets bigger and bigger. However, x can never be 0 otherwise we would have 1/0 and dividing by zero is not possible. We say that the limit of 1/x as x approaches 0 is infinity. This is because as x approaches 0, 1/x gets bigger and bigger indefinitely.
Using limits, analysis defines a myriad of other concepts used to study change. For example, differential equations is a concept feared by many students. However, it is fundamentally simple : differential equations define how a system evolves from state to state. For example, given our knowledge of the weather today, we can use differential equations to predict the weather tomorrow. Formally we ask : given the weather at time t how will it have evolved at time t+ε as ε approaches 0. In reality, the prediction we get is imperfect because our understanding of the weather of today and how it is going to change is limited, but it is enough to make predictions a few days in advance.
Geometry and topology (Study of spaces)
With arithmetic, geometry is one of the oldest and most popular forms of mathematics. It is concerned with properties of space that are related with distance, shape, size, and relative position of objects in that space. When most people hear about geometry they think of euclidean geometry a.k.a. geometry on a flat surface. However, non-euclidean geometry also exists. Geometry on the surface of a sphere is called spherical geometry. The surface of the earth can be seen in term of this geometry in which parallel line can cross; just like the lines of longitudes converges at the poles.
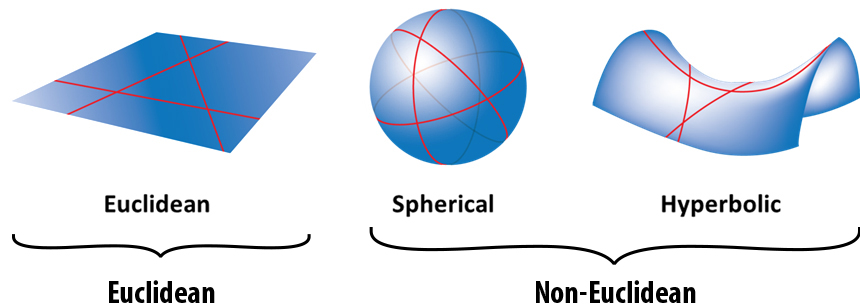
Topology on the other hand is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling and bending, but not tearing or gluing. In topology a mug and a donut are equivalent because we can transform one into the other with continuous deformations.
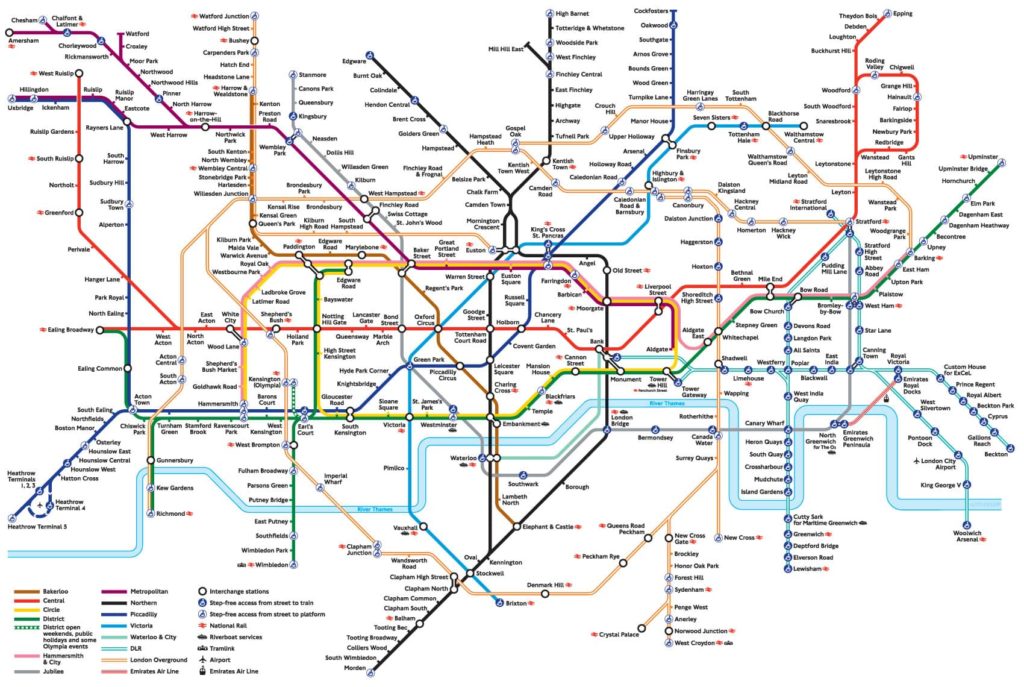
The motivating insight behind topology is that some geometric problems do not depend on the exact shape of the objects involved. If you were to draw the map of a city by hand to find a path, it does not matter if you have the exact proportion and length of the streets. As long as they are connected in the same way as in the real world, the path you are looking for will be preserved. The London metro map took this idea to its extreme by completely ignoring the geometric reality of London to propose a simple and elegant map.
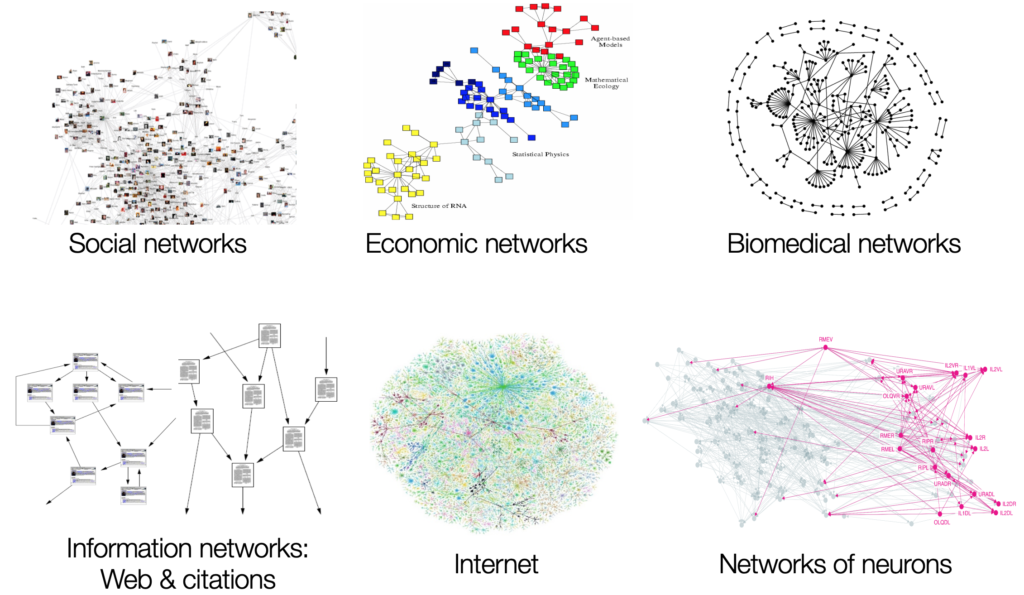
In topology, graph theory is one of my favorite fields of mathematics. Graphs are the mathematical abstraction for networks; i.e. a set of nodes connected by edges. Graphs are everywhere from social networks (people connected by friendships) to the internet (computers connected by cables) and even language (words connected by syntactic relationships). Therefore graph theory is really useful to understand our world.
[the_ad id=”1647″]
Applied mathematics
Mathematics has been widely applied in all areas of science. Computer science being one of the most prominent one to date. Computers are only possible because of our understanding of algebra, analysis, geometry and topology. Algebra makes computation possible because fundamentally computers only do simple computation such as addition, division, etc. Analysis helps with approximation. Geometry makes circuits possible. Finally, topology makes the internet work.
All other areas of science use mathematics such as physics, biology, medicine, statistics, artificial intelligence, … Thus, mathematics can be considered the most fundamental of all the sciences. Mathematics is so powerful and expressive that it not only seems to describe everything in our universe but also everything else that isn’t. The infinitesimal, for example, does not seem to exist in the real world even if its usefulness is undeniable. Incredible hidden structures were found in mathematics that no one truly understands. For example, the Mandelbrot set is an infinite art piece born from simple mathematics. It is without real purpose but infinitely beautiful.
Conclusion
With this article, I hope that I gave you a better sense of mathematics. It is a vast and complex subject which grew so large that it is impossible to learn completely in a lifetime. Click here if you wish to know more about the many subfields of mathematics.
Is your company looking to integrate AI solutions, analyze data, or strengthen its back-end development? Contact me!
Mail : pro.judicael.poumay@gmail.com
Linkedin : Judicaël Poumay
Portfolio : www.judicael-poumay.be
- ChatGPT and Large Language Models : Key Historical Milestones in AI - 22 August 2024
- Why non linearity matter in Artificial Neural Networks - 18 June 2024
- Is this GPT? Why Detecting AI-Generated Text is a Challenge - 7 May 2024
