Some infinities are bigger than others
Today I will attempt to explain simply an interesting mathematical truth about infinity and its relationship to the nature of truth.
Infinity is a characteristic rather than a number. If something is infinite, it means it does not end; its size is not finite, it cannot be measured. Yet what is more disconcerting about the infinite is that there is more than one kind and some are bigger than others. This seems absurd because you would think that to compare the size of two things you would need to measure them, but whatever is infinite is not measurable.
Comparing the size of two sets without counting
To compare the size of two sets of elements, counting is not the only solution. If we have two boxes with balls, we can indeed count the number of balls in each of them and see which box has more. But what if we do not want to count? We could take a ball from each box, pair them, and repeat this process. At the end, if the two boxes are the same size, all balls would be paired, otherwise there would be some balls leftover in one of the boxes. Hence, we do not have to count the balls to see if one box has more than the other, whichever box still contains balls is the largest.
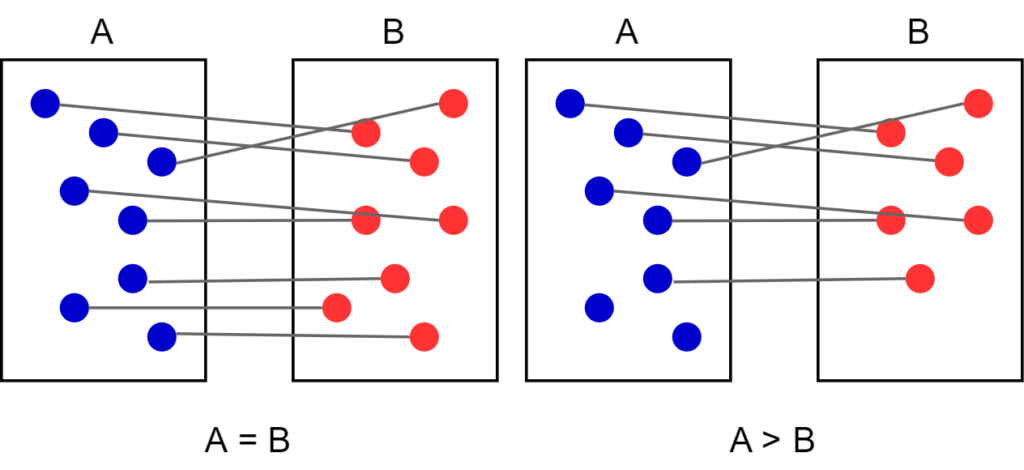
Now, let’s generalize to infinite sets of elements. Take the set of whole numbers (1,2,3,4,…) and the set of even numbers (2,4,6,8,…). In both cases they have an infinite amount of numbers; there isn’t a last number. Note that the set of whole numbers contains the set of even numbers, so you might think that the set of whole numbers is bigger, but they actually have the same size. To make sure of that, we will pair each whole number with an even number and vice-versa. Mathematically, an even number is any number divisible by two, hence we can link both set with this formula : z=2*n. Indeed, 2=2*1, 4 =2*2, 6=2*3, 8 =4*(4), … As we can see each whole number is paired with an even number with this formula, and vice-versa, demonstrating there is the same amount of both.
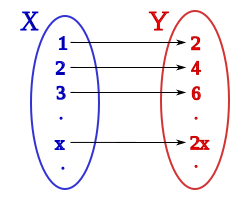
Some infinities are bigger than others
Now let’s look at two infinite sets that do not have the same size: the whole numbers (1,2,3,…) and the real numbers (1,1.0001,1.2,1.5,…). I will show you that there are many more reals than integers. One first intuition to understand is that I was able to count the whole numbers one after the other 1,2,3,… but I am not able to count the real numbers. Let’s say I start with 1, what’s next? 1.1? 1.01? 1.000000001? As you can see, There is no number after 1. Between 1 and 10 there are 10 whole numbers but there are an infinite amount of real numbers between 1 and 10. This is why we say the whole numbers are infinitely countable while the reals are infinitely uncountable. To prove more thoroughly that there are more reals than whole numbers, I will use the well-known diagonal proof proposed by Cantor, one of the great mathematicians who studied the infinite.
Imagine you could pair every whole number with a real number, as shown in the image above. On the left we enumerate all of the whole numbers and on the right for each whole number we choose a real number. Remember reals can’t be enumerated, so I had to choose them at random. Note also that this list is infinite because we try to pair all the reals and integers.
Let’s construct a new number. Even though you have used an infinite amount of whole numbers, there are still some real numbers leftover. We will find one of these real by construction. More precisely, for each whole number n, take the nth digit from its associated real number. In the image we can see that for 1 we take 1, for 2 we take 6, 3 gives us 5, etc. At the end we have the number 1.65985944… Take each digit of this number and change them to some other digit. What we get is this new number 2.76096055….
This number is not paired with any whole number. Since we changed the first digit, it can’t be the first real number in the list, but then it can’t be the second nor any of them due to its construction. This number is not paired with any whole number! Even though we paired all of them with a real already. And this number we have created is not alone; there are an infinite number of them. Indeed, there are an infinite number of ways we could have constructed such a number.
Hence, the set of real numbers is larger than the set of whole numbers. It is infinitely larger in fact and this is due to its uncountability. The real numbers are so large that after we have paired all of the whole number with a real, we still have the same amount of real leftover! We barely had to use any real number to pair them with all of the whole numbers.
Conclusion
I have proven to you that some infinities are bigger than others, you might say : “Why do we care?”. Well, this is actually extremely important because from this fact you can prove that there are some things you cannot prove to be true. In computer science we call these “undecidable problems” and in math, Gödel’s theorem of incompleteness tells a similar story. Basically, there is an infinite and uncountable amount of questions but only an countably infinite number of ways to answer these questions. While both are infinite, one is bigger than the other and thus there are questions that cannot be answered. For the curious, here is a list of known undecidable problems.
Is your company looking to integrate AI solutions, analyze data, or strengthen its back-end development? Contact me!
Mail : pro.judicael.poumay@gmail.com
Linkedin : Judicaël Poumay
Portfolio : www.judicael-poumay.be
- ChatGPT and Large Language Models : Key Historical Milestones in AI - 22 August 2024
- Why non linearity matter in Artificial Neural Networks - 18 June 2024
- Is this GPT? Why Detecting AI-Generated Text is a Challenge - 7 May 2024
