The mysteries of Neural Networks
Artificial Neural Networks are one of the most impressive discoveries of mankind. They are mathematical structures that can be taught a wide range of tasks from machine translation to image classification and better video compression algorithms. They have become ubiquitous in AI research, basically trumping most other techniques.
However, neural networks are also the most complex tools we have ever created. With models such as Switch-c and its trillion parameters, understanding what’s under the hood of these machines becomes next to impossible. This is because while we have created and trained those machines, what they have learned and how they learned it is difficult to figure out.
Hence, there are many mysteries that have come forth from the study of neural networks. We will discuss two of them : double descent and grokking.
Double descent
In class we are taught that, when developing a model such as a neural network for a task, complexity should be constrained to avoid overfitting. In other words, if a neural network is large enough, it is expected to simply learn by heart what it is taught. This is a problem because it means the model cannot generalize to new situations; they haven’t learned anything. However, a smaller network would have to learn to fit the knowledge provided into a smaller space, thus forcing it to learn patterns. For example, in a language task the model could learn (or rather discover) syntax to help it compress the information given.
However, the double descent phenomenon is a situation where the previously mentioned idea is challenged. That is, there exists indeed a good model size for which an increase or decrease would reduce performance. However, if we ignore this and continue to increase the model size, at some point, the performance improves again.
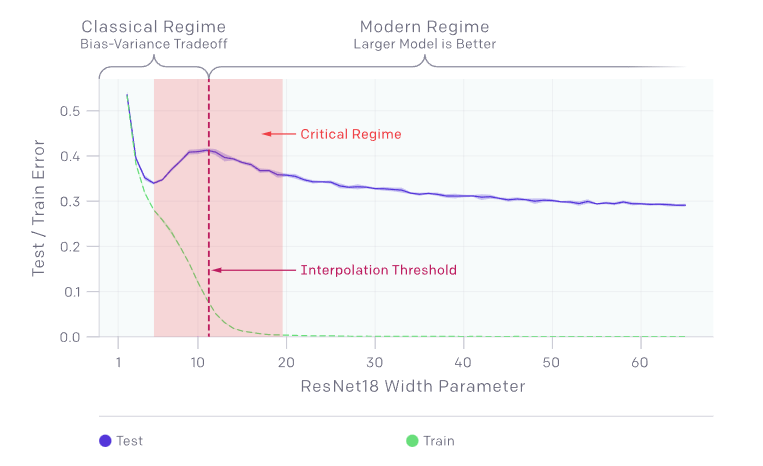
It is difficult to understand what is going on here. Why does a model big enough to learn by heart won’t take the opportunity if we make it even bigger? If it no longer makes mistakes (because it knows by heart), how does the model continue to evolve? And how is it that our previous theories hold true up until some model size?
It is noteworthy that the model size at which our previous theories break down and at which the phenomenon occurs corresponds exactly to the size needed to learn the whole training data by heart. This cannot be a coincidence, but the reason escapes us.
Grokking
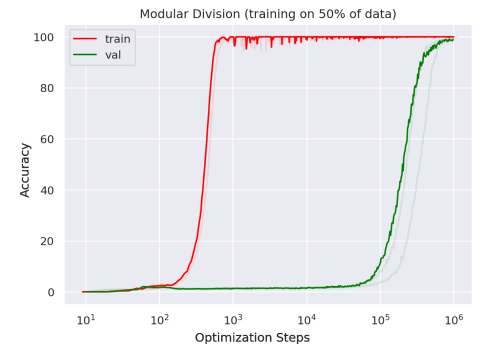
As with all good discoveries, this one was an accident. One scientist forgot to stop training their model as they went for a holiday. When they came back and realized the model was still learning they checked the results. What they found was surprising.
Grokking means to understand thoroughly and intuitively. In the context of neural networks, it is a phenomenon that is related to double descent. However, this one is even stranger. It describes a similar situation in which if we keep training a model without stopping it will eventually learn to generalize after overfitting. Most importantly, the paper shows that what the network ends up learning in the end makes perfect sense. In other words, this is not just a fluke, the model actually learned.
The difference with double descent here is two-fold. First, in scale because while their model overfits after 1000 iterations, it starts to learn correctly again after 100,000 and only after a million iterations, it actually learns nearly perfectly.
Secondly, we do not have a double descent in this case. What happens is that we have a model seemingly incapable of generalizing and initially completely overfits by learning the data by heart. Then, at some point without warning the model starts to learn. Again, one might wonder how the model managed to really learn when he had first memorized everything, but also why he did not learn earlier?
Discussion
Double descent and grokking cast doubt on our understanding of neural networks and their training procedures. These phenomena run counter to our fundamental theories that simpler models are preferable to avoid overfitting and that early termination of training is beneficial. However, we know, or at least have long observed, that larger models tend not only to perform better, but can also be trained faster than smaller models.
While these phenomena remain mysterious, understanding them could potentially lead to a revolution in the way we train neural networks, as it would be rather convenient to be able to trigger Grokking on demand or to accelerate double descent.
Is your company looking to integrate AI solutions, analyze data, or strengthen its back-end development? Contact me!
Mail : pro.judicael.poumay@gmail.com
Linkedin : Judicaël Poumay
Portfolio : www.judicael-poumay.be
- ChatGPT and Large Language Models : Key Historical Milestones in AI - 22 August 2024
- Why non linearity matter in Artificial Neural Networks - 18 June 2024
- Is this GPT? Why Detecting AI-Generated Text is a Challenge - 7 May 2024
