La Transformation de Fourier Simplifiée
Quel est le point commun entre la compression d’images, la chasse aux exoplanètes, la suppression du bruit dans un signal sonore et l’analyse moléculaire de substances ? Ces tâches apparemment sans rapport peuvent être résolues à l’aide du même outil : la transformation de Fourier. Dans cet article, nous allons voir ce qu’est la transformation de Fourier de façon simplifié et comprendre pourquoi elle est si polyvalente.
Introduction à la transformation de Fourier
En musique, chaque note a une fréquence. Dans la 4e octave, le « La » a une fréquence de 440 Hz et le « Do » 261,63 Hz. Physiquement, ces deux notes sont des ondes sinusoïdales simples. Cependant, si vous jouez ces deux notes en même temps, l’onde qui en résulte est une combinaison du « La » et du « Do », qui est une onde plus complexe, comme nous pouvons le voir ci-dessous.
Prenons maintenant cette nouvelle onde « La+Do » et soumettons-la à la transformation de Fourier. Ce que nous obtenons en retour est un nouveau graphique avec deux pics correspondant aux fréquences qui compose l’onde « La+Do ». Ces deux pics corresondent aux fréquences du « La » et du « Do ».
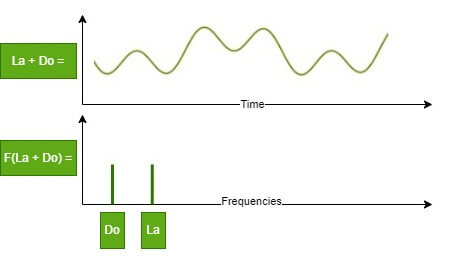
Ainsi, la transformation de Fourier nous permet de prendre une onde complexe et d’en extraire les fréquences atomiques qui la composent. Formellement, nous avons transformé l’onde originale de l’espace spatio-temporel vers l’espace des fréquences. Nous allons voir que cette idée simple a de nombreuses applications !
Compression d’images par la transformation de Fourier
Nous pouvons compresser les images en utilisant la transformation de Fourier. Prenons l’exemple d’une image en noir et blanc. Nous pouvons imaginer cette image comme une onde 2D. Plus un pixel est lumineux, plus l’amplitude sera élevée. Comme illustré ci-dessous, le reflet lumineux dans l’œil du chat correspond à une amplitude plus élevée que le noir de la pupille.
Nous pouvons observer que certaines parties d’une image ont plus de détails que d’autres. La fourrure du chat présente de nombreux changements de luminosité par rapport à son nez. Par conséquent, lorsque l’on considère une image comme une onde, les zones très détaillées correspondent à des ondes de fréquence plus élevée. Alors que les zones avec peu de details où la luminosité ne change pas beaucoup correspondent à des ondes de plus basse fréquence.
Par conséquent, plus une image est détaillée, plus elle contient d’ondes de haute fréquence. Ainsi, une façon de compresser une image est de supprimer ces hautes fréquences. En ne conservant que les fréquences plus basses, on garde une image moins détaillée mais aussi plus légère en mémoire.
Puisqu’une image peut être vue comme une onde, la transformation de Fourier nous permet de transformer une image en ses fréquences atomiques. Maintenant que nous sommes dans l’espace des fréquences, nous pouvons simplement sélectionner et éliminer les ondes de haute fréquence. Ensuite, nous pouvons retransformer les fréquences restantes en une image. Et voilà, c’est ainsi que JPG compresse les images !
Ci-dessous, nous pouvons voir l’image du chat où nous avons supprimé plus de 90% des hautes fréquences. L’image est de moins bonne qualité mais la taille en mémoire est passée de 160KB à 4KB. Vous pouvez voir comment les poils de la fourrure du chat ne sont plus visibles mais nous reconnaissons toujours le chat.
Autres applications de la transformation de Fourier
Nous pouvons également utiliser la transformation de Fourier pour chasser les exoplanètes ! Lorsque deux corps sont en orbite l’un autour de l’autre, ils tournent autour d’un centre de masse commun. Ainsi, lorsqu’une planète tourne autour d’une étoile, nous pouvons voir l’étoile osciller. Si nous avons plusieurs planètes, chacune d’entre elles fera osciller l’étoile un peu différemment. En observant une étoile, nous pouvons voir cette oscillation et la traduire en une onde.
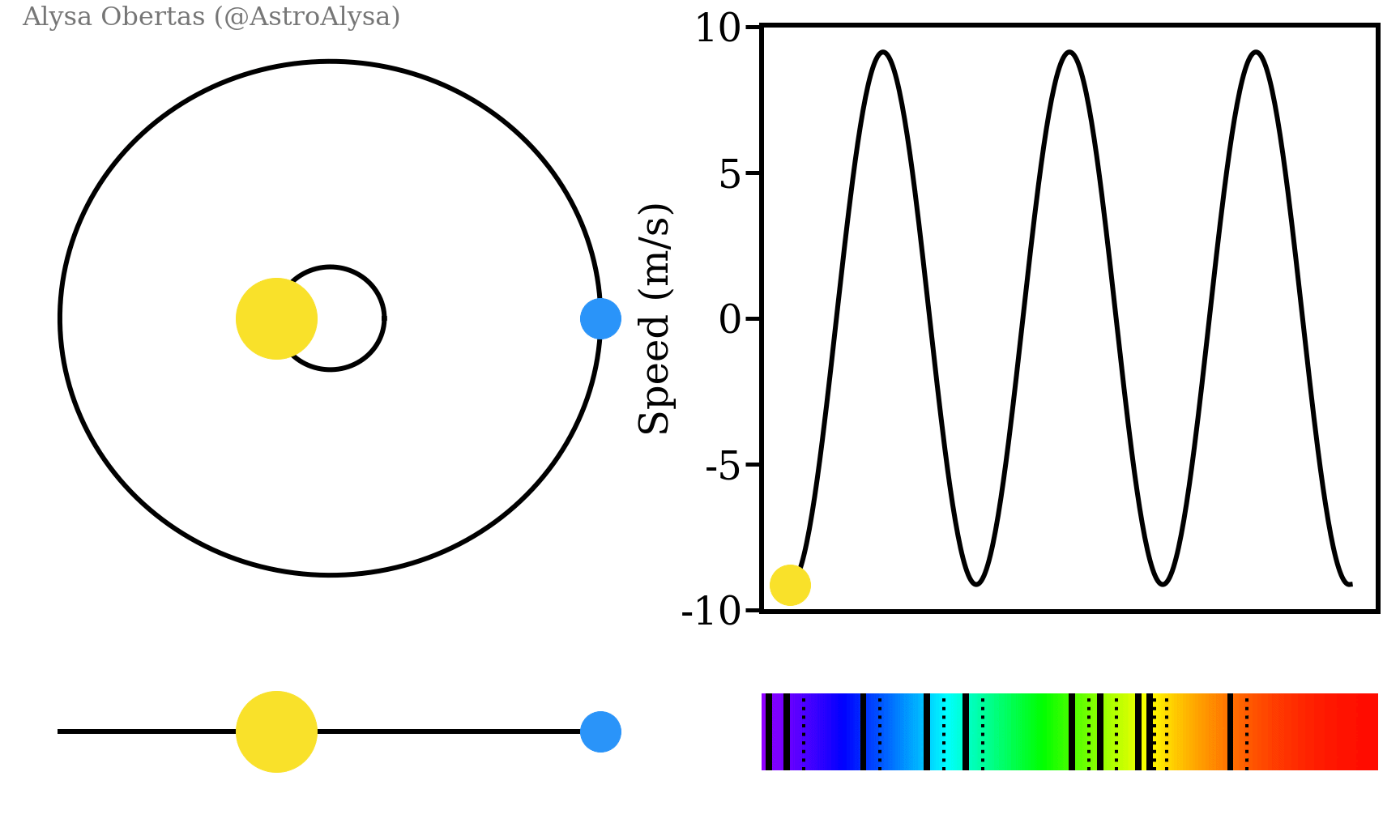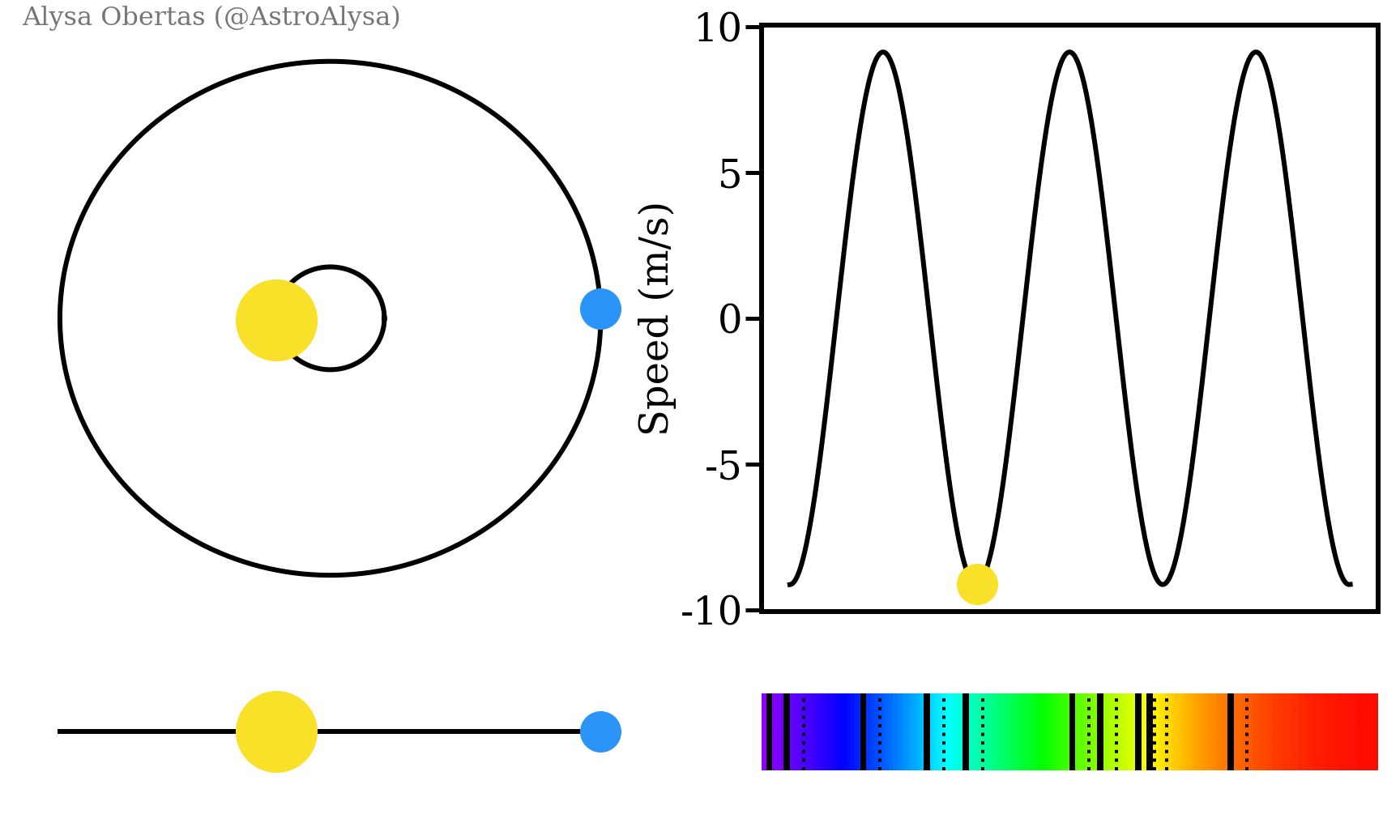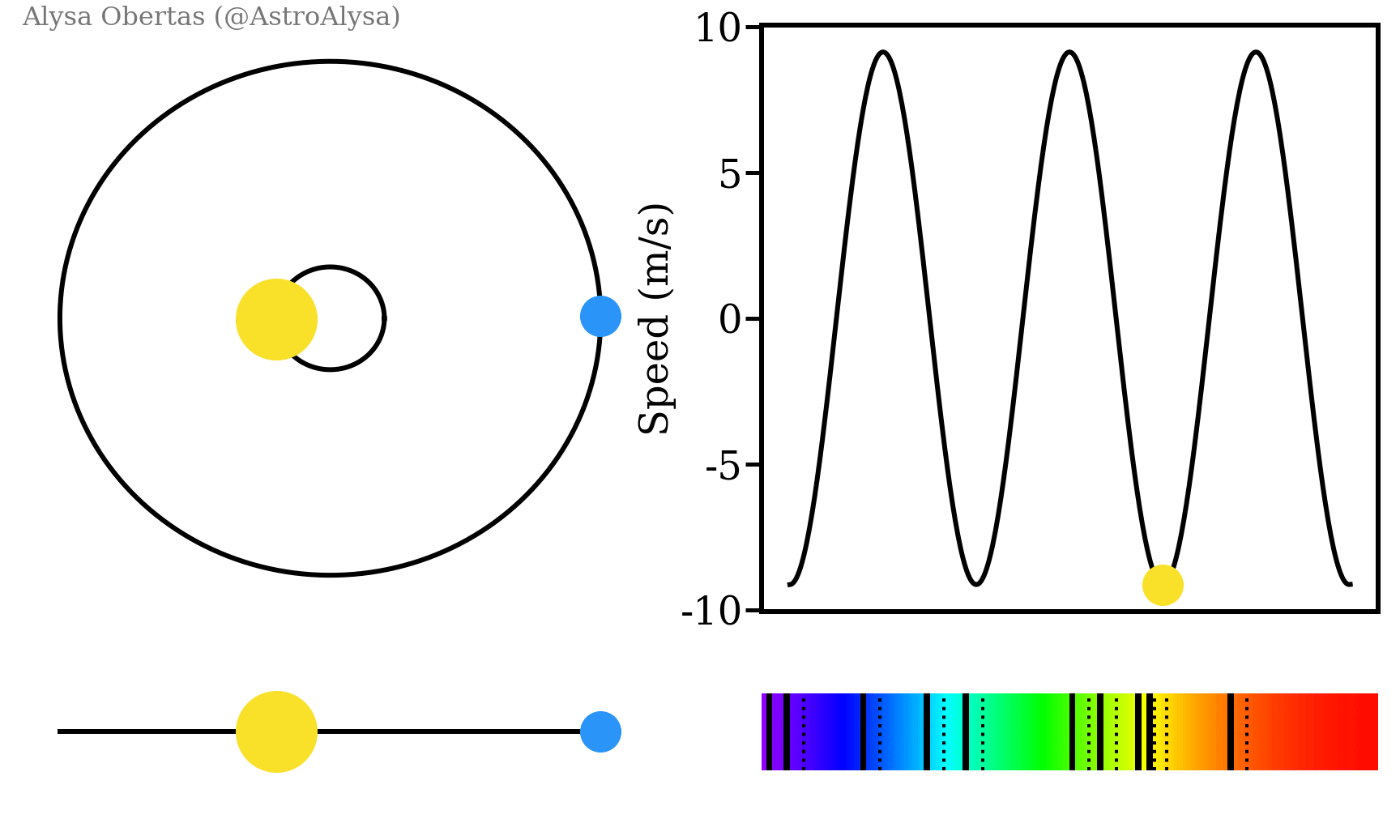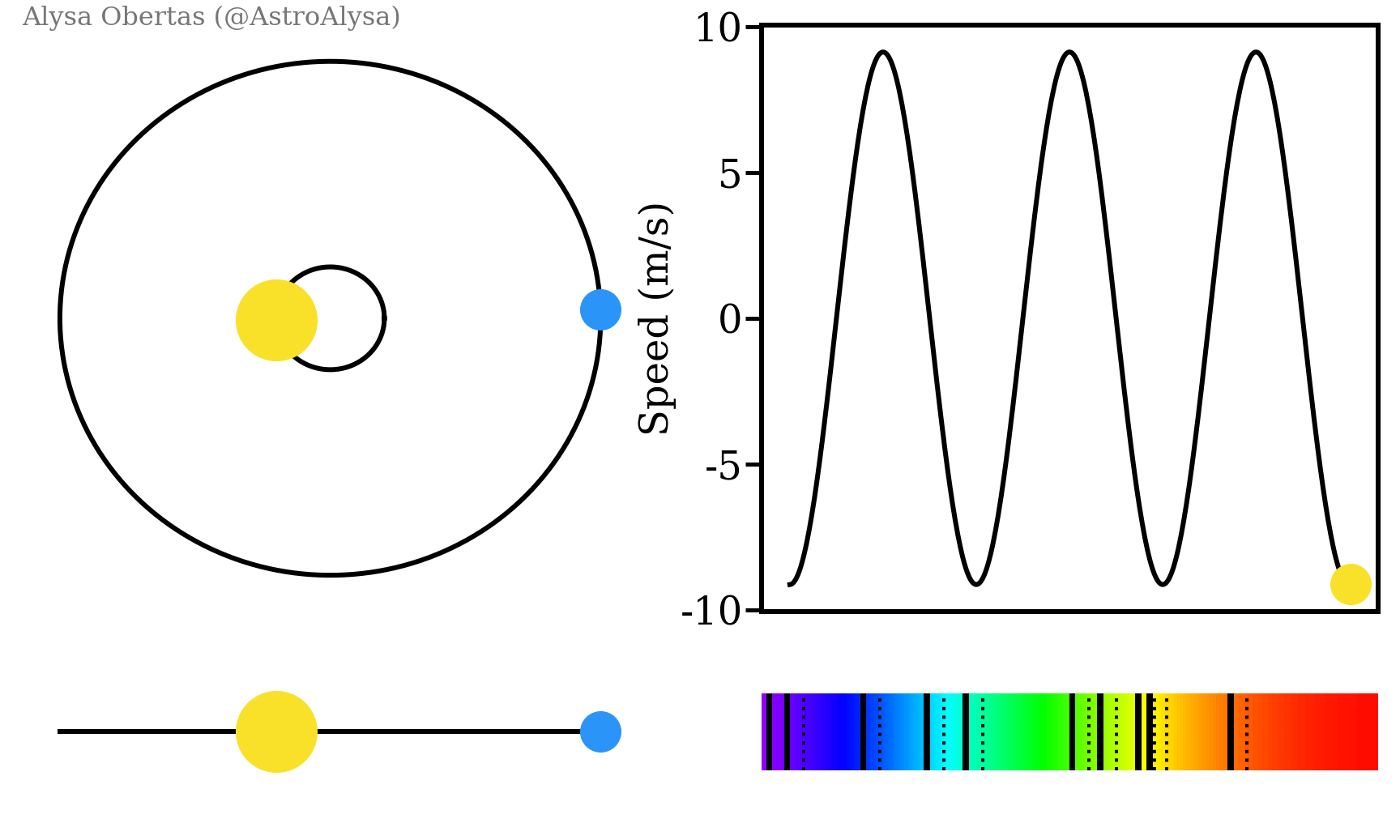
Si l’on applique la transformation de Fourier à cette onde, chaque fréquence extrait correspond à une planète. Les planètes qui sont plus proches orbitent plus rapidement et correspondent à des fréquences plus élevée. L’amplitude de chaque fréquence nous donne également le rapport entre la masse de l’étoile et celle de la planète, car des planètes plus massives entraîneront une plus grande oscillation de l’étoile.
En analyse moléculaire, nous pouvons envoyer un faisceau de lumière sur une substance et analyser la lumière réfléchie. Vu que la lumière est une onde, la transformation de Fourier est aussi très utile ici! Différent atomes/molécules vont absorber et réfléchir différents types de lumière. En appliquant la transformation de Fourier à la lumière réfléchie, nous pouvons donc extraire les fréquences qui composent cette lumière, chacune d’entre elles correspondant à un élément spécifique composant la substance. ce procédé s’appelle la Spectroscopie.
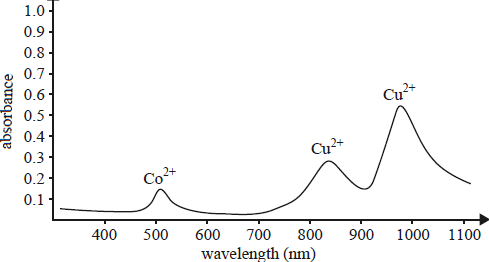
Finalement, dans le traitement du signal, le bruit correspond souvent à des fréquences plus élevées. Là encore, nous pouvons utiliser la transformation de Fourier pour transformer un signal et éliminer facilement ces fréquences. Nous pouvons ensuite reconvertir le signal dans l’espace d’origine et voila nous avons supprimé le bruit. C’est ce qu’on appelle un filtre passe-bas. Il est utilisé pour nettoyer les sons enregistrés par un microphone dans une zone bruyante ou pour nettoyer les signaux électriques à l’intérieur d’un processeur.
Conclusion
La transformation de Fourier est un véritables couteau suisse mathématique. Elle peut être utilisées dans presque tous les domaines, du traitement d’images à la chasse aux exoplanètes en passant par l’analyse de la composition chimique des substances. Comme vous avez pu le voir, la transformation de Fourier est l’une des découvertes mathématiques les plus importantes à ce jour. Pouvez-vous imaginer d’autres applications de la transformation de Fourier ? J’espère vous voir dans les commentaires 😉
Votre entreprise cherche-t-elle à intégrer des solutions d'IA, à analyser des données ou à renforcer son développement back-end ? Contactez-moi !
Mail : pro.judicael.poumay@gmail.com
Linkedin : Judicaël Poumay
Portfolio : www.judicael-poumay.be
