Les branches des mathématiques
Les mathématiques, qu’on les aime ou qu’on les déteste, elles dirigent notre monde. Elles forment les fondations de toutes les sciences, de l’informatique à la biologie en passant par l’économie. C’est le langage de l’univers et de tout ce qu’il contient. Cependant, à moins d’étudier les mathématiques au niveau universitaire, on pourrait penser que les mathématiques ne sont qu’une question de chiffres. C’est pourquoi, je souhaite vous présenter les trois branches principales des mathématiques : l’algèbre, l’analyse et la géométrie / topologie. Ne vous inquiétez pas, le but n’est pas de plonger dans la complexité des domaines mais plutôt de vous donner une idée de leur importance.
L’algèbre (l’étude des structures mathématiques)
L’algèbre est l’étude des structures mathématiques et de leur interaction; c’est l’étude des formules, des équations, … C’est l’étude de la façon d’écrire les mathématiques.
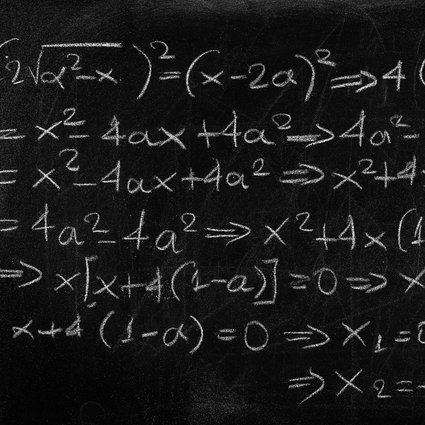
Le sous-domaine le plus connu de l’algèbre est l’arithmétique, « l’art des nombres ». Il s’agit de l’étude des nombres et de leur interaction par le biais d’opérations telles que l’addition, la division, la multiplication, etc. C’est le sous-domaine le plus populaire des mathématiques dans le sens où il peut être utile à chacun dans sa vie quotidienne. Par exemple, quand nous allons faire des courses ou que nous planifions un itinéraire vers une destination, l’arithmétique nous est utile pour nous aider à tenir compte de l’argent et du temps consacrés à ces activités.
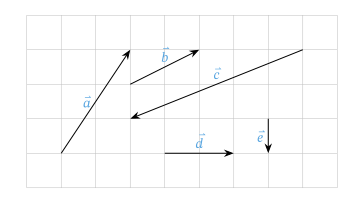
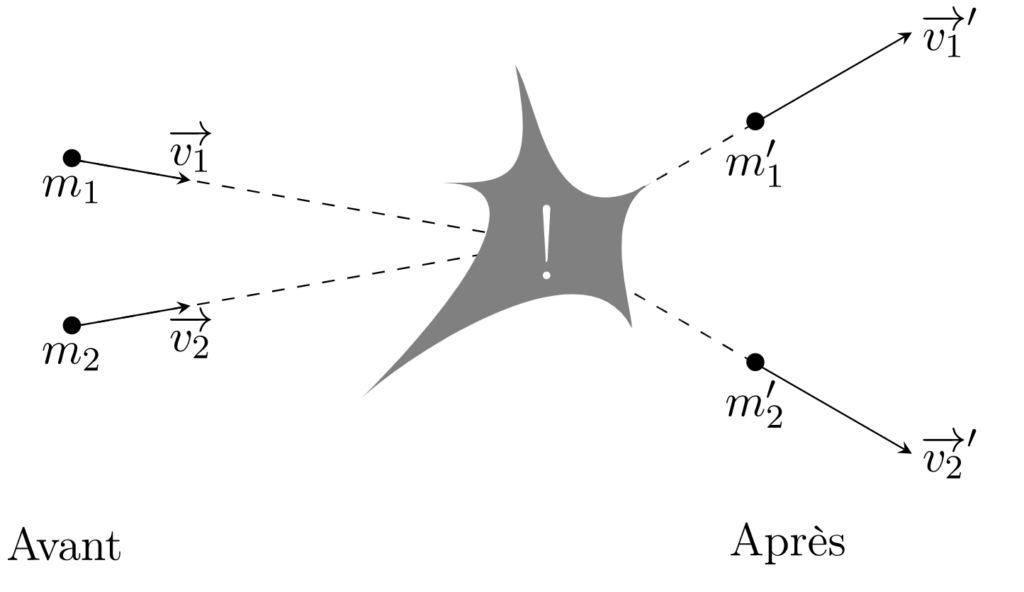
Un autre sous-domaine de l’algèbre est l’algèbre linéaire. Simplement, il s’agit de l’étude des vecteurs et de leur interaction. Un vecteur décrit une direction et une amplitude; ils sont représenté par des flèches. Ils constituent un élément essentiel des mathématiques modernes et sont utilisés dans de nombreuses applications. Ils peuvent être utilisés pour décrire une force appliquée sur un objet, la vitesse d’une voiture, ou l’évolution du prix d’un bien. En physique par exemple, les vecteurs permettent de grandement simplifier les calculs de collisions
L’analyse (l’étude des changements)
L’analyse est l’étude du changement et des concepts connexes. L’analyse pose des questions telles que : « qu’est ce qui se passe lorsque le plus petit changement possible est appliqué? ». Le plus petit changement possible n’est pas zéro mais il est aussi proche de zéro que possible, nous appelons cela un changement infinitésimal.
Vous vous demandez peut-être : Quel genre de changements ? Des changements de quoi ? Eh bien de tout et n’importe quoi, c’est le but des mathématiques, de tout modéliser. Par exemple, les changements de prix des biens pour l’économiste ou les changements de forces appliquées sur un objet pour le physicien.
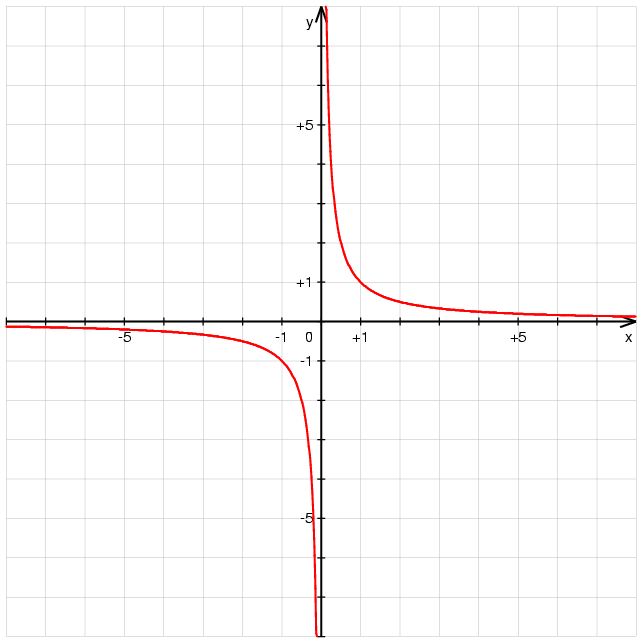
Pour étudier ces changements, nous utilisons les limites; une valeur dont on peux s’approcher mais que l’on peux rarement atteindre. Un bon exemple est 1/x, car quand x devient de plus en plus petit, 1/x devient de plus en plus grand. Cependant, x ne peut jamais être 0 sinon nous aurions 1/0 et la division par zéro n’est pas possible. Nous disons que la limite de 1/x lorsque x se rapproche de 0 est l’infini. Car plus x se rapproche de 0, plus 1/x devient grand, et ce indéfiniment.
En utilisant les limites, l’analyse définit beaucoup d’autres concepts utilisés pour étudier les changements. Par exemple, les équations différentielles sont un concept redouté par de nombreux étudiants. Cependant, c’est fondamentalement simple : les équations différentielles définissent comment un système évolue d’un état à l’autre. Par exemple, étant donné notre connaissance de la météo d’aujourd’hui, nous pouvons utiliser les équations différentielles pour prédire la météo de demain. Formellement, nous nous demandons : étant donné la météo au moment t, comment aura-t-elle évolué au moment t+ε lorsque ε s’approche de 0. En réalité, la prévision que nous obtenons est imparfaite car notre compréhension de la météo actuelle et de la façon dont elle va changer est limitée, mais nous en savons suffisamment pour faire des prévisions quelques jours à l’avance.
Géométrie et topologie (l’étude des espaces)
Avec l’arithmétique, la géométrie est l’une des formes les plus anciennes et les plus populaires des mathématiques. Elle s’intéresse aux propriétés de l’espace comme la distance, la forme, la taille ou encore la position relative des objets dans cet espace. Quand la plupart des gens entendent « géométrie », ils pensent à la géométrie euclidienne, c’est a dire la géométrie des espaces plat. Cependant, il existe aussi une géométrie non euclidienne. La géométrie de la surface d’une sphère est appelée géométrie sphérique. La surface de la terre correspond a cette géométrie dans laquelle des lignes parallèles peuvent se croiser; tel les lignes de longitudes qui convergent aux pôles.
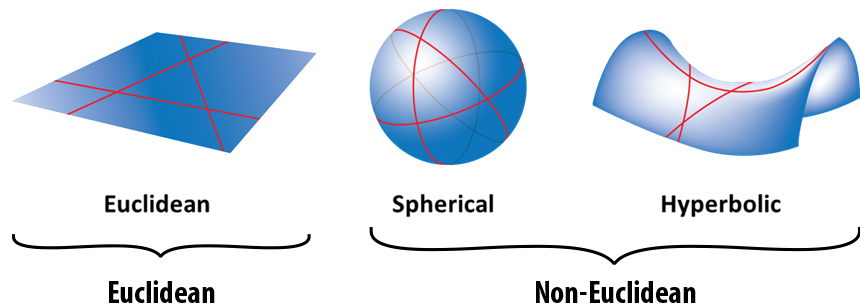
La topologie, en revanche, s’intéresse aux propriétés d’un objet géométrique conservées sous déformations continues, telles que l’étirement, la torsion, le froissement et le pliage, mais pas la déchirure ou le collage. En topologie, une tasse et un donut sont équivalents car on peux arriver de l’un a l’autre par déformation continues.
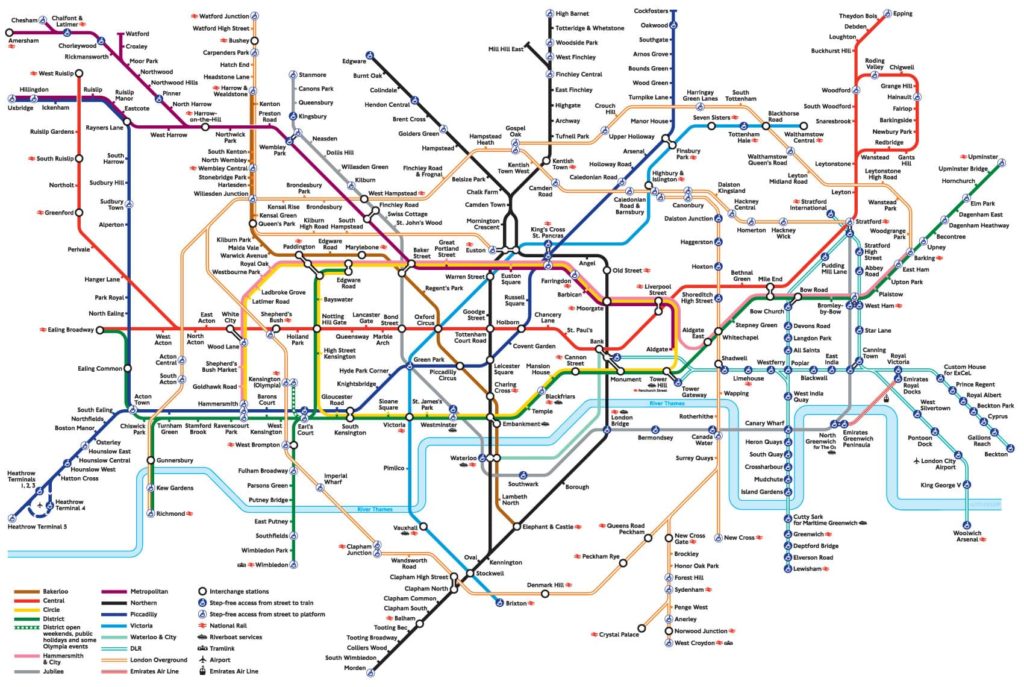
L’idée derrière de la topologie est que certains problèmes géométriques ne dépendent pas de la forme exacte des objets concernés. Si vous deviez dessiner le plan d’une ville à la main pour trouver un chemin, peu importe que vous ayez la proportion et la longueur exactes des rues. Tant qu’elles sont reliées de la même manière que dans le monde réel, le chemin que vous cherchez sera préservé. La carte du métro de Londres a poussé cette idée à l’extrême en ignorant complètement la réalité géométrique de Londres pour proposer une carte simple et élégante.
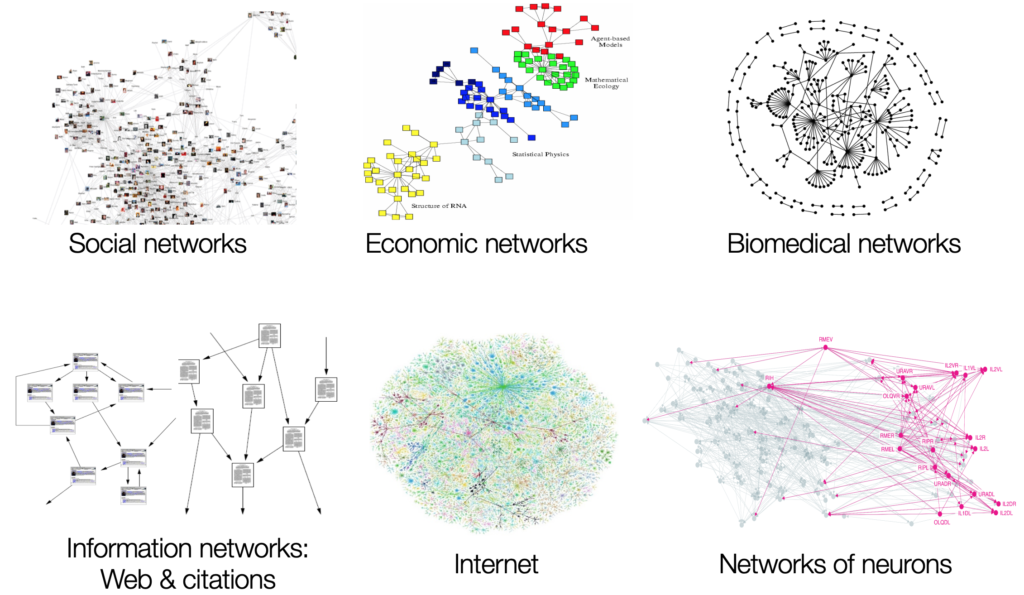
En topologie, la théorie des graphes est l’un de mes domaines mathématiques préférés. Les graphes sont l’abstraction mathématique des réseaux, c’est-à-dire un ensemble de nœuds reliés par des liens. Les graphes sont partout, des réseaux sociaux (personnes connectées par des amitiés) à internet (ordinateurs connectés par des cables) et même dans les langues (mots connectés par des relations syntaxiques). La théorie des graphes est donc très utile pour comprendre notre monde.
[the_ad id= »1647″]
Mathématiques appliquées
Les mathématiques ont été largement appliquées dans tous les domaines de la science. L’informatique étant l’un des plus importants à ce jour. Les ordinateurs ne sont possibles que grâce à notre compréhension de l’algèbre, de l’analyse, de la géométrie et de la topologie. L’algèbre rend le calcul possible car, fondamentalement, les ordinateurs ne font que des calculs simples tels que l’addition, la division, etc. L’analyse aide à l’approximation. La géométrie rend les circuits imprimé possibles. Enfin, la topologie permet a internet de fonctionner.
Tous les autres domaines de la science utilisent aussi les mathématiques, comme la physique, la biologie, la médecine, les statistiques, l’intelligence artificielle, … Ainsi, les mathématiques peuvent être considérées comme la plus fondamentale de toutes les sciences. Les mathématiques sont si puissantes et expressives qu’elles semblent non seulement décrire tout ce qui se trouve dans notre univers, mais aussi tout ce qui ne s’y trouve pas. L’infinitésimal par example ne semble pas exister dans le monde réel même si son utilité est indéniable. Nous avons trouvé dans les mathématiques d’incroyables structures cachées que personne ne comprend vraiment. Par exemple, l’ensemble de Mandelbrot est une œuvre d’art infinie née de simples mathématiques. Elle est sans véritable but mais infiniment magnifique.
Conclusion
Avec cet article, j’espère vous avoir donné un aperçu des mathématiques. C’est une matière vaste et complexe qui a pris une telle ampleur qu’il est impossible de l’étudier complètement en une vie. Cliquez ici si vous souhaitez en savoir plus sur les nombreux sous-domaines des mathématiques.
Votre entreprise cherche-t-elle à intégrer des solutions d'IA, à analyser des données ou à renforcer son développement back-end ? Contactez-moi !
Mail : pro.judicael.poumay@gmail.com
Linkedin : Judicaël Poumay
Portfolio : www.judicael-poumay.be
2 Comments
Laisser un commentaire
Ce site utilise Akismet pour réduire les indésirables. En savoir plus sur comment les données de vos commentaires sont utilisées.
Il semble que les mathématiques ne sont pas destinées à assurer un bon orthographe :
« … pour être informer des nouveaux articles » !!!
« … pour être informé des nouveaux articles »
Hum !
Aie! Effectivement, l’orthographe a toujours été ma bête noir^^
Merci de m’en informer!