Certains infinis sont plus grands que d’autres
Aujourd’hui, je vais tenter d’expliquer simplement un concept mathématique particulièrement intéressant a propos de l’infini.
L’infini est une caractéristique plutôt qu’un nombre. Si une chose est infinie, cela signifie qu’elle ne fini pas; sa taille n’est pas finie, elle ne peut pas être mesurée. Mais ce qui est encore plus déconcertant à propos de l’infini, c’est qu’il en existe plus d’une sorte et que certain infinis sont plus grands que d’autres. Cela semble absurde car on pourrait penser que pour comparer la taille de deux choses, il faudrait les mesurer, mais ce qui est infini n’est pas mesurable.
Comparer la taille de deux ensembles sans les mesurer
Pour comparer la taille de deux ensembles d’éléments, mesurer leur taille n’est pas la seule solution. Si nous avons deux boîtes avec des boules, nous pouvons en effet compter le nombre de boules dans chaque et voir quelle boîte en contient le plus. Mais que faire si nous ne pouvons pas compter ? Nous pourrions prendre une boule dans chaque boîte, les associer par paires et répéter ce processus. À la fin, si les deux boîtes sont de la même taille, toutes les boules seraient mis en paire, sinon il resterait quelques boules dans l’une des boîtes. Il n’est donc pas nécessaire de compter les boules pour voir si une boîte en contient plus qu’une autre.
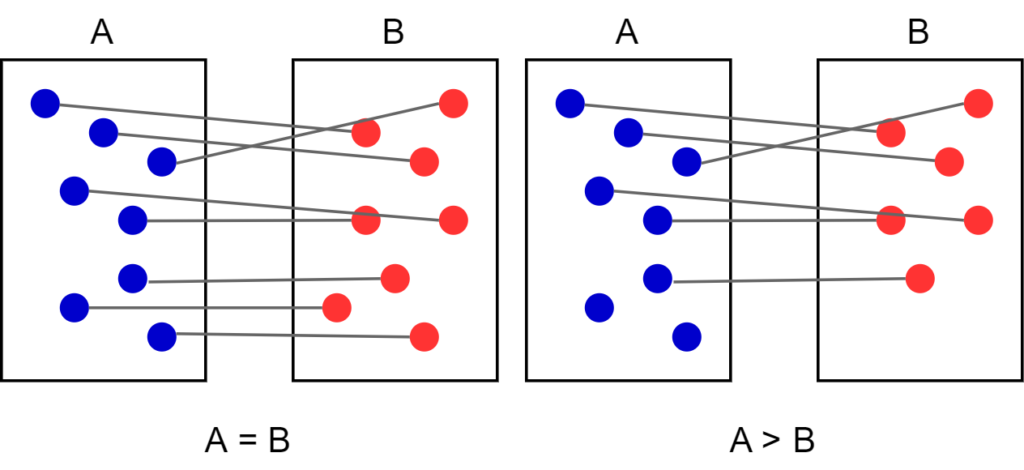
Maintenant, généralisons aux ensembles infini d’éléments. Prenez l’ensemble des nombres entiers (1,2,3,4,…) et l’ensemble des nombres pairs (2,4,6,8,…). Dans les deux cas, il y a une quantité infinie de nombres; il n’y a pas de dernier nombre. Notez que l’ensemble des nombres entiers contient l’ensemble des nombres pairs, donc vous pourriez penser que l’ensemble des nombres entiers est plus grand, mais en fait ils ont la même taille. Pour s’en assurer, nous allons associer chaque nombre entier à un nombre pair et vice-versa. Mathématiquement, un nombre pair est un nombre divisible par deux, d’où la possibilité de lier les deux ensembles avec cette formule : z=2*n. En effet, 2=2*1, 4 =2*2, 6=2*3, 8 =4*4, … Comme on peut le voir, chaque nombre entier est associé à un nombre pair avec cette formule ce qui démontre qu’il y a la même quantité des deux.
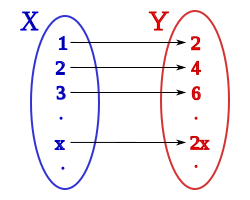
Certains infinis sont plus grands que d’autres
Examinons maintenant deux ensembles infinis qui n’ont pas la même taille : les nombres entiers (1,2,3,…) et les nombres réels (1,1.0001…,1.2…,3.1415…,…). Je vais vous montrer qu’il y a bien plus de réels que d’entiers. Une première intuition pour comprendre est que j’ai pu compter les nombres entiers l’un après l’autre 1,2,3,… mais je ne suis pas capable de compter les nombres réels. Disons que je commence par 1, et ensuite ? 1.1 ? 1,01 ? 1.000000001 ? Comme vous pouvez le voir, Il n’y a pas de nombre après 1. Entre 1 et 10, il y a 10 nombres entiers, mais il y a une quantité infinie de nombres réels entre 1 et 10. C’est pourquoi nous disons que les nombres entiers sont infiniment dénombrable alors que les réels sont infiniment indénombrable. Pour prouver de manière plus rigoureuse qu’il y a plus de réels que de nombres entiers, je vais utiliser la fameuse preuve en diagonale proposée par Cantor, l’un des grands mathématiciens qui a étudié l’infini.
Imaginez qu’il est possible d’associer chaque nombre entier à un nombre réel, comme le montre l’image ci-dessus. À gauche, nous énumérons tous les nombres entiers et à droite, pour chaque nombre entier, nous choisissons un nombre réel. N’oubliez pas que les nombres réels ne peuvent pas être énumérés, j’ai donc du les choisir au hasard. Notez aussi que cette liste est infini car on essaye de mettre en paire tout les réels et les entiers.
Construisons un nouveau nombre. Même si nous avons utilisé une quantité infinie de nombres entiers, il reste encore quelques nombres réels. Nous allons trouver l’un de ces réel par construction. Plus précisément, pour chaque nombre entier n, prenons le nième chiffre du nombre réel qui lui est associé. Sur l’image, nous pouvons voir que pour 1, nous prenons 1, pour 2, nous prenons 6, 3 nous donne 5, etc. À la fin, nous avons le nombre 1.65985944… Ensuite, prenez chaque chiffre de ce nombre et changez-les avec un autre chiffre. Ce que nous obtenons est un nouveau nombre : 2.76096055….
Ce nombre n’est pas associé à un nombre entier. Etant donné que nous avons changé le premier chiffre, il ne peut pas être le premier réel de la liste, mais il ne peut pas être le deuxième ni aucun d’entre eux a cause de sa construction. Ce nombre n’est pas associé à un nombre entier! Même si nous les avons déjà tous associés à un réel. Et ce nombre que nous avons créé n’est pas seul ; il y en a une infinité. En effet, il y a une infinité de façons dont nous aurions pu construire un tel nombre.
Par conséquent, l’ensemble des nombres réels est plus grand que l’ensemble des nombres entiers. Il est en fait infiniment plus grand, et cela est dû à son caractère non dénombrable. Les nombres réels sont si grands qu’après avoir associé tous les nombres entiers à un réel, il nous reste toujours la même quantité de réels ! Nous n’avons pratiquement pas eu besoin d’utiliser de nombre réel pour les associer à tous les nombres entiers.
Conclusion
Maintenant que je vous ai prouvé que certaines infinités sont plus grandes que d’autres, vous pourriez dire : « quel est l’intérêt? » Eh bien, c’est en fait extrêmement important parce qu’à partir de ce fait, vous pouvez prouver qu’il y a certaines choses que vous ne pouvez pas prouver. En informatique, nous appelons cela des « problèmes indécidables » et en mathématiques, le théorème d’incomplétude de Gödel raconte une histoire similaire. Fondamentalement, il existe une quantité infinie et indénombrable de questions, mais seulement un nombre infiniment dénombrable de façons d’y répondre. Si les deux quantité sont infinies, l’une est plus grande que l’autre et il y a donc des questions auxquelles on ne peut pas répondre. Pour les curieux, voici une liste de problèmes indécidable.
Votre entreprise cherche-t-elle à intégrer des solutions d'IA, à analyser des données ou à renforcer son développement back-end ? Contactez-moi !
Mail : pro.judicael.poumay@gmail.com
Portfolio : www.portfolio.thethoughtprocess.xyz
Spinoff project : www.aiashi.be
- La révolution des Chatbots et de l’IA : Interview - 25 mars 2024
- La révolution des Transformers : Comment l’IA à été démocratisé - 21 février 2024
- Comment GPT Révolutionne le Monde de l’Intelligence Artificielle - 1 février 2024
