Réseau de neurones simplifié partie 3 : apprentissage
Ce qui différencie l’intelligence artificielle (IA) des autres programmes informatiques est leur capacité à apprendre ; leur comportement n’est pas seulement décidé par les programmeurs mais aussi par leur propre expérience. C’est pourquoi l’IA peut nous surpasser dans de nombreuses tâches. Dans cet article, je vais essayer de vous montrer comment les réseaux neuronaux apprennent.
Que veux-t-on dire par entraîner un réseaux de neurones?
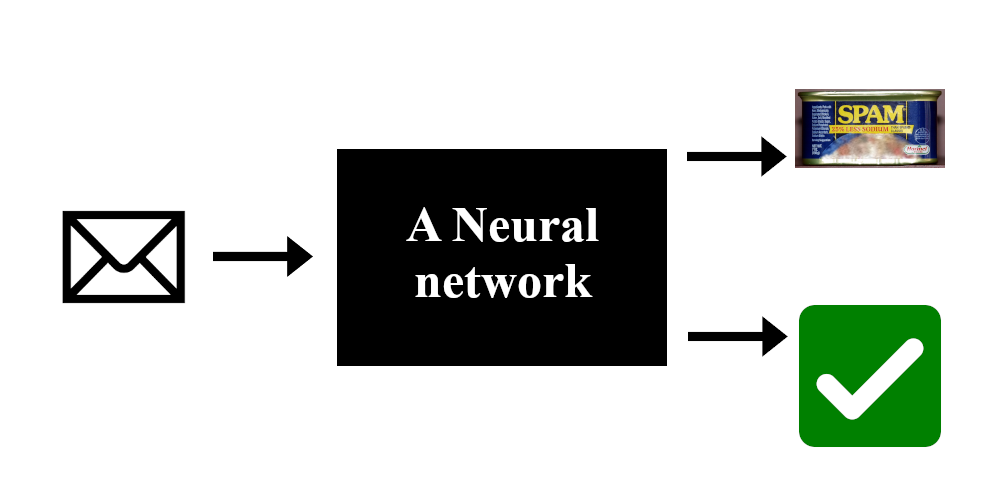
Rappelons nous du premier article où je présentais un simple réseaux de neurones pour classifier des mails comme spam ou non spam. Ce type de réseaux prend certains nombres en entrée et en produit d’autres en sortie. Ici, l’entrée représente un mail (style, orthographe, grammaire, …) et la sortie représente à quel point le réseau pense que ce mail est un spam.
Dans le premier article, j’ai également expliqué comment les réseaux prennent des décisions. Pour résumer, les neurones sont liés et ces liens ont un poids associé. Le poids de chaque lien détermine la force avec laquelle l’information passe d’un neurone à l’autre. Ainsi, les poids définissent entièrement le comportement du réseau de neurones.
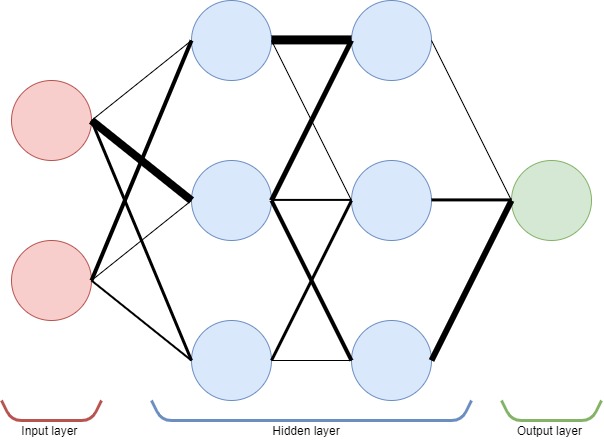
Entraîner un réseau, c’est trouver un arrangement de poids, où certains neurones sont plus fortement liés que d’autres, de sorte que le réseau prenne de bonnes décisions. Notez que de nombreuses configurations de poids peuvent conduire à la même performance en raison de la symétrie interne du réseau.
Apprentissage supervisé
L’apprentissage supervisé est un moyen d’entraîner les réseaux de neurones. Cela signifie que nous utilisons des données étiquetées pour entraîner notre réseau. Dans ce cas, imaginez que nous ayons 10000 mails étiquetés manuellement par quelqu’un comme étant spam ou non. Nous présenterons ces données au réseau afin qu’il puisse apprendre à différencier les deux types de courrier.
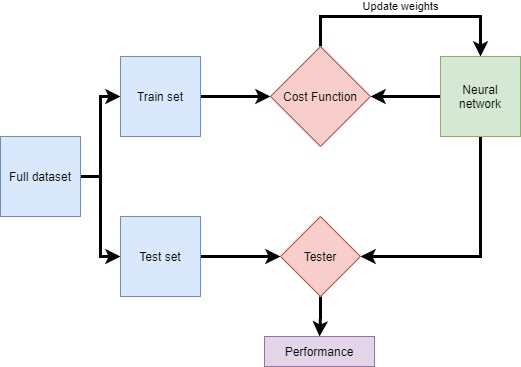
En pratique, nous découpons généralement ces données en plusieurs ensembles. Un ensemble d’entrainement est utilisé pour entraîner le réseau et un ensemble de test est utilisé pour tester ses performances. En effet, puisque le réseau est formé sur l’ensemble d’entrainement, il connaît les données et sera plus performant sur celui-ci. Ainsi, le fait de conserver un ensemble de test séparé garantit que le réseau est testé sur des données qu’il n’a jamais vues. Cela permet de mieux mesurer les performances du réseau.
L’influence des poids sur l’erreur
Ce que nous voulons, c’est réduire l’erreur globale que fait le réseau. Il s’agit ici de réduire les erreurs de classification de mails. Imaginez une machine qui prend en compte les poids actuel d’un réseaux et calcul l’erreur pour un ensemble d’entraînement donné; cette machine est appelée la fonction de coût. Ce que nous voulons donc, c’est minimiser la fonction de coût en choisissant une meilleur configuration de poids.
Les poids sont un ensemble de chiffres. Imaginez d’abord qu’il n’y en ait qu’un seul. À tout moment, nous pouvons augmenter ou diminuer ce poids, ce qui aura une incidence sur la valeur de l’erreur totale. Par conséquent, il existe pour ce poids au moins une valeur qui conduit à l’erreur la plus faible (indiquée par un X vert sur le graphique ci-dessous). En pratique, nous n’avons pas un poids mais souvent des millions mais l’idée reste la même : il y a une courbe d’erreur et un point où elle est la plus faible et le but est de le trouver.
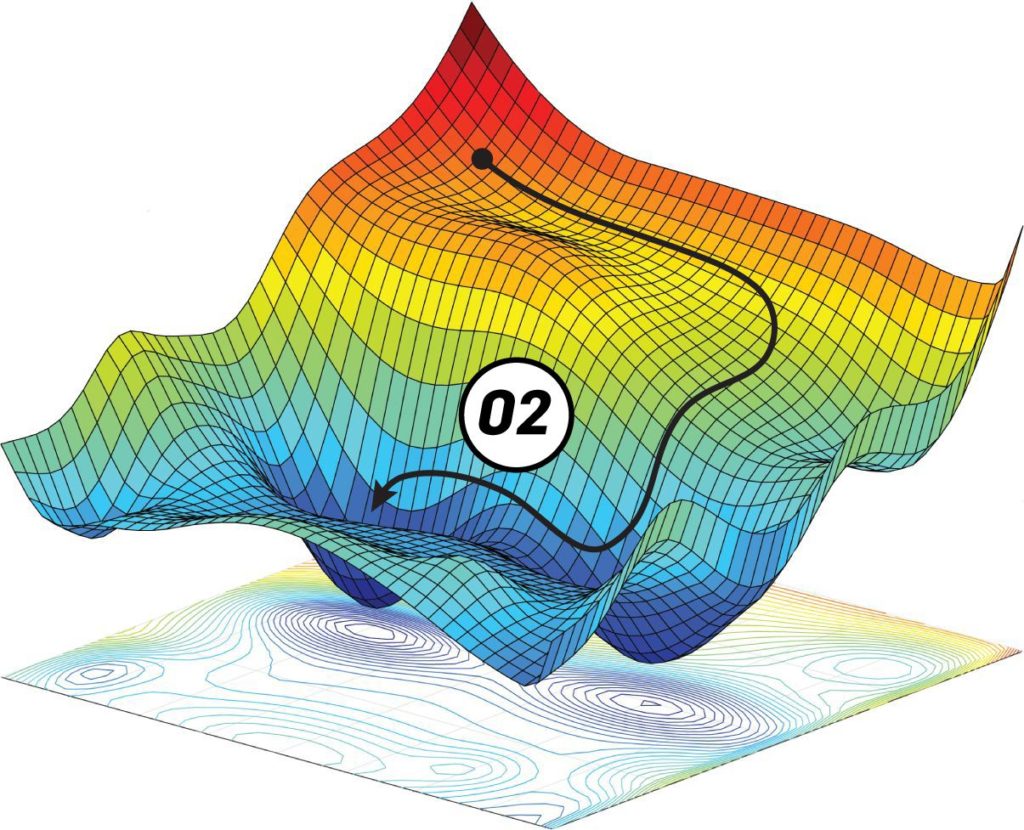
En théorie nous pouvons dessiner la fonction de coût mais en réalité nous ne pouvons connaître que l’erreur pour des configurations de poids qui on été testée. Cela signifie que nous ne savons pas à quoi ressemble la fonction de coût. Par conséquent, nous ne savons pas tout de suite quelle est la meilleure configuration de poids. Nous avons donc besoin de protocoles d’entraînement pour chercher la configuration de poids qui conduit à de bonnes performances.
[the_ad id= »1647″]
Protocoles d’entraînement
Une approche naïve consiste à tester de nombreuses configurations de poids choisies au hasard et prendre la meilleure, mais cela est très lent et inefficace. Une meilleure approche encore est la descente de gradient. Je n’entrerai pas dans les détails mais ici la magie des mathématiques nous donne un bel outil : le gradient. Les gradients peuvent nous donner la direction de la descente locale pour une fonction donnée. Ainsi, il n’est pas nécessaire de regarder dans quelques directions. Nous avons maintenant un bon moyen de réduire l’erreur en suivant ce gradient, c’est rapide à calculer et beaucoup plus efficace. Si l’on suit le gradient, nous somme garantie d’atteindre un minimum local de la fonction de coût.
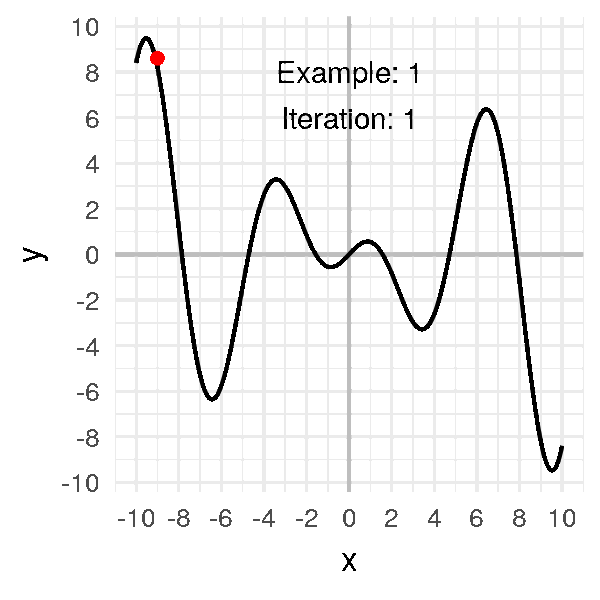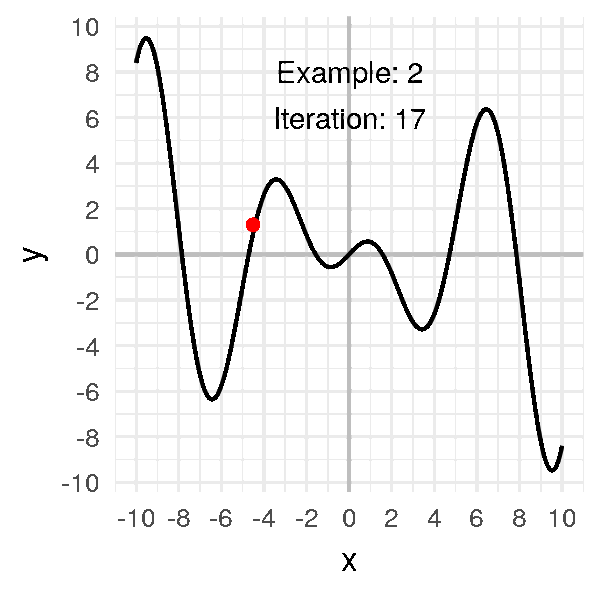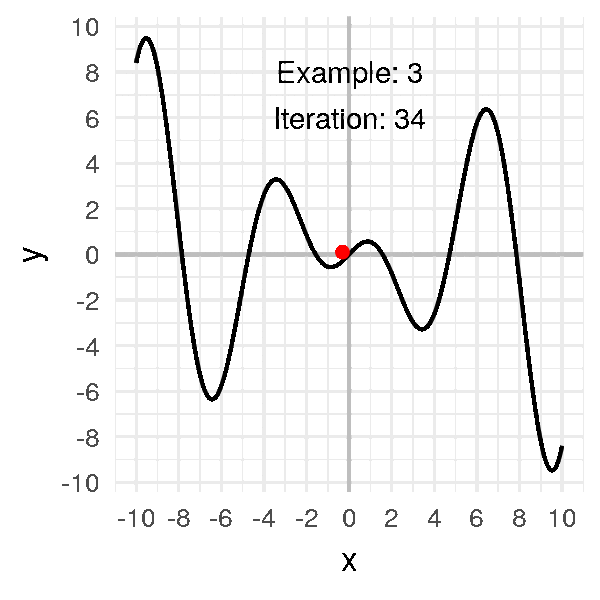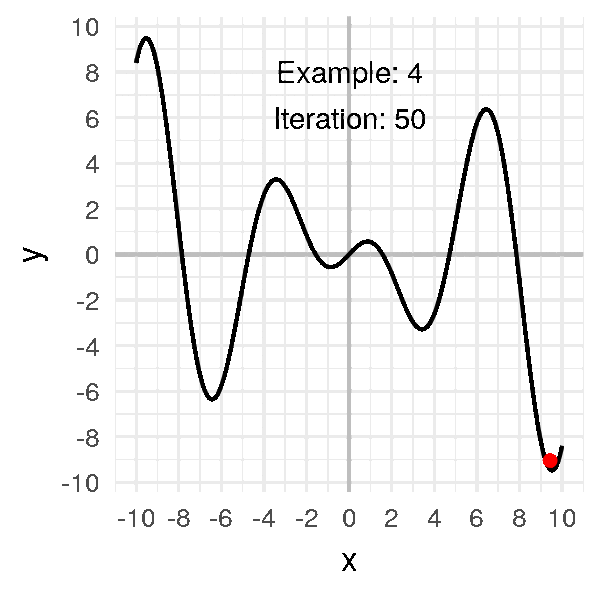
L’un des gros problèmes des méthodes de descente est que nous risquons de nous retrouver coincés dans un minimum local. En effet, la fonction de coût a une forme complexe et il y a beaucoup de vallées et de dunes. Nous voulons descendre dans la vallée la plus basse, mais nous ne pouvons voir que localement. Par conséquent, si nous sommes dans un minimum local, nous sommes coincés là parce que la seule façon de s’en sortir est de grimper. Nous ne pouvons pas grimper parce que nous voulons descendre et souvenez-vous qu’en pratique, vous ne savez pas à quoi ressemble la courbe d’erreur complète.
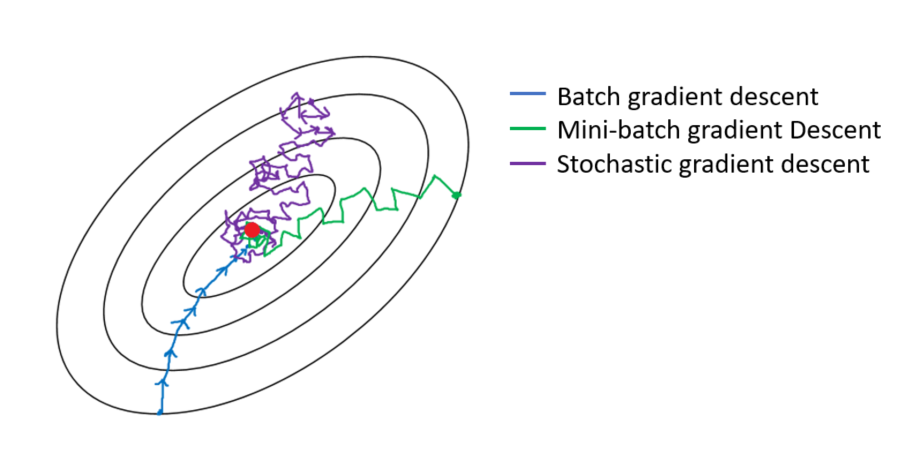
La descente stochastique de gradient a été inventée pour pallier ce problème. Encore une fois, n’entrons pas dans les détails mais imaginons qu’au lieu que la courbe d’erreur soit statique, nous la faisons vibrer avec une certaine intensité. Cela signifie que parfois, lorsqu’on est coincé dans une petite vallée, une vague arrive et la vallée devient une colline dont on peut tomber. La courbe d’erreur vibre juste un peu et garde toujours une forme assez similaire, de sorte que les grandes vallées ne disparaissent pas et que seules les petites sont touchées. Cette solution est beaucoup plus efficace car elle nous permet d’éviter de rester bloqué dans certains minima local. Elle est à la base de la plupart des protocoles d’apprentissage actuellement utilisés. malgré tout, la formation de certains réseaux peut prendre des semaines.
Conclusion
Les réseaux neuronaux doivent apprendre. Cela signifie qu’il faut trouver un ensemble de poids afin de minimiser la fonction de coût. À l’aide de données étiquetées, nous pouvons utiliser des protocoles d’entraînement tels que la descente stochastique de gradient pour trouver un bon ensemble de poids. Cela correspond à l’exploration d’une surface afin de trouver la vallée la plus basse.
Oh, je vois que vous avez lu jusqu’à la fin. Merci pour votre soutien; j’espère que cette série est intéressante. Si vous voulez bricoler avec des réseaux, je vous suggère d’aller sur ce site où vous pourrez vous amuser avec un réseaux simple et quelques jeux de données. Amusez-vous à ajouter des couches, des neurones, à tester des trucs, etc. C’est fun, je vous le recommande vivement.
Votre entreprise cherche-t-elle à intégrer des solutions d'IA, à analyser des données ou à renforcer son développement back-end ? Contactez-moi !
Mail : pro.judicael.poumay@gmail.com
Linkedin : Judicaël Poumay
Portfolio : www.judicael-poumay.be
